What is the Rarest Raga?

Using math to keep Carnatic concert-goers happy and to explain why the janya-janaka system of classifying ragas is useful.

Picture this. It is 6:30pm on a Tuesday. A remarkable assortment of mamas and mamis have gathered for the prime Carnatic Music concert (kutcheri) of the day. The mamas, who are dressed in their shiniest kurtas, have eagerly occupied the front-row seats. Some have even come prepared to participate in the music creation by loudly humming with the artists on stage. The mamis, less boisterous, have dropped their evening poojas to be here, so are naturally more expectant.

As the kutcheri unfolds, it becomes clear that the performance is failing to meet the high expectations of the audience. The mamas shift restlessly. The check-shirted mama closest to the stage whips out his flip-cased Redmi to listen to the latest WhatsApp voice recording (it seems Ramesh’s son is looking for suitors). The mamis might let out the occasional “sabaash” (an appreciative exclaim), but only when her astute neighbour does.

By the end of the evening, the atmosphere is one of mild discontent. The sentiment is captured in the post-concert commentary; “somaaraa irindidu” or “parvagilla” is the consensus.

Their complaint: there were no rare ragas sung.

It is a story I see all too often. The run-of-the-mill ragas no longer cut it. An artist is evaluated not just on her ability to belt out a 30-minute rendition of Kalyani (a popular raga), but also the freshness of her concert list. Mami isn’t wrong to expect this. Infact, as a rasika (keen listener) myself, I can’t deny that I pay a little more attention when a rarer raga is attempted. Presenting a rare raga well is difficult; the absence of regular patterns to settle in, large note jumps, and unusual vakra (zig-zag) patterns means that a rare raga requires a syllabus of its own.

It’s not just mama, mami and I. According to Vid. R Vedavalli, as expressed in a 2013 lecture demonstration, 'the capacity to innovate with new ragas is the paramount element that sets our music apart'. In 2007, Baradwaj Rangan wrote a piece in Sruti magazine on the music’s trend towards these ragas, wherein Sikkil Gurucharan called it a “welcome change”. Artist Vivek Sadashivam, on his Instagram page, puts up short clips under the title “Rare Ragas Series”. Rare ragas are, at the very least, a source of major intrigue.

---

I (in jest) propose the following: if audience excitement peaks when a rare raga is presented, then to maximise audience satisfaction, artists must present the rarest raga.

---

Ragas and Rarity

A raga is a melodic guideline. Typically, each raga has a structured scale with two parts: an aarohanam (an ordered set of notes present on an ascent) and an avarohanam (an ordered set of notes present on a descent). Compositions and improvisations set to tune in these ragas, while not tightly bound by its scale, at least play gracefully and irregularly with its notes and order.

There are 7 swaras (fundamental musical units). Some swaras have tonal variations. Today, the convention in notations is that there are 16 possible notes (tonal variations) within an octave in Carnatic Music, with 12 unique notes (some pairs within the 16 have the same tonal frequency but are functionally different). They are:

Sa: S
Ri: R1, R2, R3
Ga: G1, G2, G3
Ma: M1, M2
Pa: P
Da: D1, D2, D3
Ni: N1, N2, N3

Frequency equivalents:
R2 = G1
R3 = G2
D2 = N1
D3 = N2

Consider the following three ragas:

dheerashankaraabharaNam: (popularly known just as "shankaraabharaNam")
- Aarohanam: S R2 G3 M1 P D2 N3 S
- Avarohanam: S N3 D2 P M1 G3 R2 S

bEgaDa:
- Aarohanam: S G3 R2 G3 M1 P D2 N3 D2 P S
- Avarohanam: S N3 D2 P M1 G3 R2 S

nirOSTa:
- Aarohanam: S R2 G3 D2 N3 S
- Avarohanam: S N3 D2 G3 R2 S

A regular concert attendee might rank these on their popularity in concerts in the order that they appear here: Shankarabharanam, then Begada, and then Niroshta. It is a factor of many things: the number of compositions you hear in these ragas, their proclivity to be picked as a main raga in a kutcheri, the fact that Shankarabharanam is full-octave raga (it contains one version of every note) and the other two’s notes are derived from it. We’ll explore few of these parameters, and at each step we’ll use these three ragas to evaluate our metric for rarity.

Number of Compositions and Rarity

I found a lovely dataset of compositions on GitHub compiled by Srihari Sriraman here. It came with a list of ragas too. The original source for these is likely the well-known Raga Pravaham book compiled by musicologists Dr. Dhandapani and D. Pattammal. Credits and laddoos to all of them.

A raga could be rare if there are very few compositions set to tune in it. However, one quickly realizes that around 92% of ragas do not list any composition under it. Carnatic music is rather boutique, and we will never truly know how many compositions there are, even those good enough to be sung at a decent concert. So even if we assume that half of these ragas have unlisted compositions, we are still no closer to finding the rarest raga.

I plot the number of compositions by raga in descending order. The curve looks negative exponential. So, we can perhaps find the most ubiquitous ragas but not the rarest.

---

Digression:

As a sort of back-of-the-napkin calculation. I fit the number of compositions by raga with a power law distribution, to measure whether there is an inequality in how compositions were distributed between ragas. Amongst ragas that have at least one composition, 80% of compositions come from just 25% of ragas. In more complicated terms, the pareto exponent was estimated to be α  = ~3.32 (3). As a comparison, the pareto exponent for income inequality around the world usually lies between 1.5 to 3 (the lower it is, the more unequal the distribution). Other things that have an α = 3 are the number of citations that scientific papers published in 1981 received between their publication date and June 1997 (Redner, 1998) and the diameters of craters on main-belt asteroids (Ivanov et. al, 2001). Perhaps not quite the smoking gun, but hopefully there is a stark enough inequality here for a certain handsome left-handed mridangist to soon write an impassioned article on.

---

Scales and Rarity

A raga could be rare if its underlying patterns are infrequently borrowed by other ragas. Here it starts to get a little math-y. I’ll use something called a bigram.

I’ll explain bigrams through an example of sentence structure. If I gave you the word “he”, and asked you whether the word “lemon” would likely appear as the next word, you’d probably say no. You’d reason, based on the corpus of English that you’ve read or heard, that you’ve never encountered such a word combination before (unless your corpus is Wodehouse). If there were a sentence that contained “he lemon”, you’d find that sentence unusual and possibly rare. “Lemon” on its own is not weird to encounter, but it is the fact that we have information about what word came just before it which made it weird.

We learn two things from this. Rarity of something is related, in an inexact way, to the frequency (rather, the infrequency) of occurrence of its component parts and contextual to what came before it. So, if we can figure out from the dataset of all English the probabilities of words that come after the word “he” by their frequency of occurrence, you can identify the lemons so-to-speak, or the ones that are rarer. We can continue this process now with the word “lemon”. Unlikely to follow “lemon” is “winter”, and so on. Multiplying each probability of occurrence with each other, we’ll get a rarity score. We have now found the joint probability of the words occurring in that order. This is the principle behind a bigram.

\(P('he') \cdot P('lemon' | 'he') \cdot P('winter' | 'lemon') ... \)

Bigrams are a part of a broader class of models called N-gram models (taking N words/tokens prior to determine the next one). No less an AI mahaan than Dr. Subbarao Kambhampati called ChatGPT and other LLMs “N-gram models on steroids”. While we are interested in the rarest ragas, ChatGPT is interested in finding the most appropriate (therefore, non-rare) next word to display. He speculates that ChatGPT is kind of 3000-gram, which means it takes context from the last 3000 words in order to produce the next one. (Warning: This is a serious oversimplification. Less simplified version here.)

(I’ve employed here the writing trick called apophenia, where I said some rather disconnected things and you’ve connected them. Now you’ve likened this kutti project to ChatGPT. Thank you.)

For ragas, each note does depend on the note we saw before it. For example, we can expect R1 to follow S in the aarohanam, but it would be unusual to see D2 follow S.

Let’s take Shankarabharanam. We’ll start with the aarohanam. We have to begin somewhere, so we find the base probability of “S” occurring contextless. 98% of the aarohanams begin with “S”. Now, we find the probability that “R2” occurs when “S” precedes it. It does so 31% of the time. Continue until the list ends at the higher octave “S”. We’ll do the same for the avarohanam. I take the geometric mean of the scores from the aarohanam and avarohanam to average the complexity generated between the two.

\(\text{rarity}_{\text{aarohanam}} = p_{S} \cdot p_{S \rightarrow R2} \cdot p_{R2 \rightarrow G3} \cdot p_{G3 \rightarrow M1} \cdot p_{M1 \rightarrow P} \cdot p_{P \rightarrow D2} \cdot p_{D2 \rightarrow N3} \cdot p_{N3 \rightarrow Ṡ}\)

\(\text{rarity}_{\text{avarohanam}} = p_{Ṡ} \cdot p_{Ṡ \rightarrow N3} \cdot p_{N3 \rightarrow D2} \cdot p_{D2 \rightarrow P} \cdot p_{P \rightarrow M1} \cdot p_{M1 \rightarrow G3} \cdot p_{G3 \rightarrow R2} \cdot p_{R2 \rightarrow S}\)

\(\text{rarity}_{\text{raga}}= \sqrt{rarity_{aarohanam} \cdot rarity_{avarohanam}}\)

I found that Srihari’s dataset of ragas was too precise. Different schools learn different scales for the same raga, so I wanted to be able to choose from a list of possible scales to pick the most appropriate one. So, I decided to scrape this lovely page from Karnatik.com and used Srihari’s dataset and other sources as corroborating evidence. Links to everything are at the end.¹

On this dataset, I apply our formula onto every raga. Accordingly, here are the top 10 least rare ragas:

And here are the top 10 rarest ragas:

Super cool!

While I recognise a few of the least rare ragas, I was so floored by the rarest ones. If you are familiar with reading notations, do take a moment to look silly while you try to sing them aloud.

A quick hygiene check. Shankarabharanam has a score of 0.002593, while Niroshta has a score of 0.000118, an order of magnitude rarer. However, Begada, which we expect to rank in between the two, scores around 10^-6. It seems that this is happening because scores are being influenced by the length of the aarohanam and avarohanam. The more probabilities there are to multiply, the smaller the eventual score. Shivamanohari seems to have profited from this, with its two noted aarohanam.

To fix this, we can take the overall geometric mean of the joint probabilities of each the aarohanam and avarohanam. This will average out the rarity contributed by each note transition. The inverse of this gives us a measure called perplexity. LLM people use this to test language models, and to decide the most appropriate N to use in their N-gram model. Read a good technical note here.

For Shankarabharanam,

\(\text{newrarity}_{\text{aarohanam}} = \left( p_S \cdot p_{S \rightarrow R2} \cdot p_{R2 \rightarrow G3} \cdot p_{G3 \rightarrow M1} \cdot p_{M1 \rightarrow P} \cdot p_{P \rightarrow D2} \cdot p_{D2 \rightarrow N3} \cdot p_{N3 \rightarrow Ṡ} \right)^{\frac{1}{8}}\)

\(\text{newrarity}_{\text{avarohanam}} = (p_{Ṡ} \cdot p_{Ṡ \rightarrow N3} \cdot p_{N3 \rightarrow D2} \cdot p_{D2 \rightarrow P} \cdot p_{P \rightarrow M1} \cdot p_{M1 \rightarrow G3} \cdot p_{G3 \rightarrow R2} \cdot p_{R2 \rightarrow S})^{\frac{1}{8}}\)

\(\text{newrarity}_{\text{raga}}= \sqrt{newrarity_{aarohanam} \cdot newrarity_{avarohanam}}\)

I’ll quickly reflect on what it means to be the least rare raga. The least rare ragas, using our chosen measure, will have patterns of consecutive notes that appear most frequently in other ragas as well. But intuitively, if they were necessarily non-rare, we’d hope to recognise more of them. This takes me to something larger.

In Carnatic music, a contentious topic is the janya-janaka system of understanding ragas. It propounds, based on the scales of ragas, that some ragas (janyas) are derived from others (janakas). And this theory is quite old. Prof. Sambhamurthy says that this system “crystallised into a definite form in the fourteenth century” (Source). Govindaracharya proposed a Melakarta system that groups all 72 possible full-octave scales (linear symmetric scales with one variation of each swara) together. Today, we consider each melakarta as a janaka raga, and through an irregular method, we’ve allocated other ragas under them. By artificially assigning non-melakarta ragas a melakarta janaka, some scholars argue that we’ve straightjacketed our understanding of ragas. While I know none who give this system unequivocal support, others with an opposing view argue that it is a useful stepping-stone framework for young learners.

Given all this, the results from our perplexity-based model are out-of-seat-jumpingly interesting.

Here are the new top 10 least rare ragas:

And, here are the new top 10 rarest ragas:

7 out of the top 10 least rare ragas are melakarta ragas!

The list of reasons why Harikambhoji is special never ends, least of which is that the Mixolydian mode, a Western counterpart to Harikambhoji, is the basis for Lorde’s “Royals,” The Beatles’ “Norwegian Wood”, and Beyoncé’s “Single Ladies.”

The Melakarta system makes some sense!

It is often argued that the janya-janaka system is arbitrary. In an effort to classify one under the other, we often obscure the true essence of a raga for little value add. I found an old lecture demonstration where artists debated this system:

Most take a hedging view towards the system. Given the tenor of the conversation, it may be useful to ponder over what the system can actually do well. This section is a response only to the argument that the melakarta raga as a janaka raga does not give us a representative understanding of ragas classified under it and is therefore arbitrary.

Artist Chitravina Ravikiran makes the counterargument that as a formula for basic understanding, this melakarta-janya system allows students of the music to see individual notes from an unknown raga and, almost like a shape sorter toy, identify what melakarta it might fit under. Or at least learn what melakarta it does not fit in. I like to think of this as the first sieve you put a raga under to gain a measure of understanding about it.

However, we reasoned earlier that each note in a scale is contextual to what came before it. So, if we want to go one step further, and if we expect the melakarta system to be revelatory, each pair of consecutive notes in an unknown raga, at some level, must relate to pairs of notes in its melakarta.

Consider the following logic: if a melakarta raga is truly the first sieve, then we expect it to be the simplest possible representation/sequence of its notes relative to its janyas. Every other raga that is classified under a melakarta must necessarily be more complex. If a janya raga was less complex compared to its melakarta, then putting it through the sieve is an obfuscation and does not give us some higher-level understanding of the raga.

What I mean by “complex” here is “less frequent”. I understand that a raga like Hamsadhwani might be more straightforward than its listed melakarta Kalyani because it has fewer notes, but the note omissions (G3 → P, P → N3) are less frequently observed in other ragas. One could imagine that the simpler structure would be the scale of Kalyani, from which we take away some notes, to get something more complex.

Using the language of the project, we expect the janyas to be rarer (i.e more complex) than the melakarta it is listed under based on our perplexity-based model. I plot here the comparison between the rank of the janya compared to its listed melakarta:

Out of a dataset of 4411 ragas, only 28 are less complex compared to its melakarta. A staggeringly low 0.63% error rate. This is the best part! 9 out of the 28 are Asampoorna Melakartas (alternate method of raga classification)! I can’t think of anything more beautiful than both the big-ticket melakarta classifications appearing together! Perhaps a more optimal classification of ragas might actually include a mixture of the two. What a world!

The melakarta-janya system need not be the most optimal classification of ragas. But its system is so simple, and, by at least one measure, useful that it deserves more credibility. This framework need not explain every raga under it. It instead acts as a first level of granularity on top of which innate features of the raga can be explored. I do question the current nomenclature: calling one the parent of the other implies lineage and hierarchy. Many have pointed out that Kambhoji is classified under Harikambhoji, although it is much older.

Some of the finer details of the system need ironing out. Scholars dispute which janaka certain ragas must fall under. As it appears in my dataset, Hindolam is classified under Hanumatodi. All scholars nod in the video at the suggestion that it is better classified under Natabhairavi, given similarities in the raga lakshana (a crude translation would be “raga essence”). It happens that either way Hindolam will be more “complex” than its parent. Anyway, who knows how many such disputed classifications there are in my dataset? Mathematically, I must also check my claim’s validity under trigrams, 4-grams and more (I think, however, that the number of ragas is too small to get valid results from it). But if you agree that a scale is a sequence of notes each depending on at least the previous note, then the melakarta system as a first measure of looking at other ragas is useful.

Other Findings

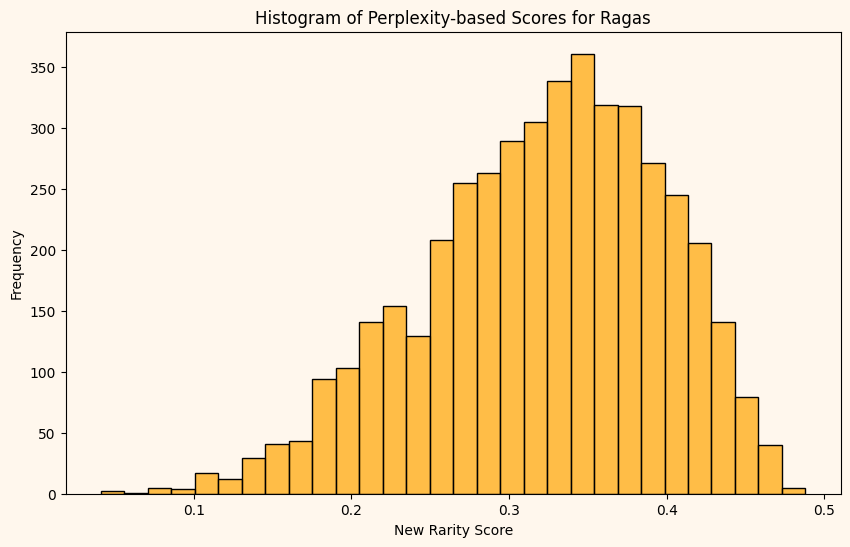
• I plot a histogram of our perplexity-based rarity. Neatly distributed. I have been scouring the data endlessly to explain that sudden drop between 0.2 and 0.3, but no success as of yet.

  

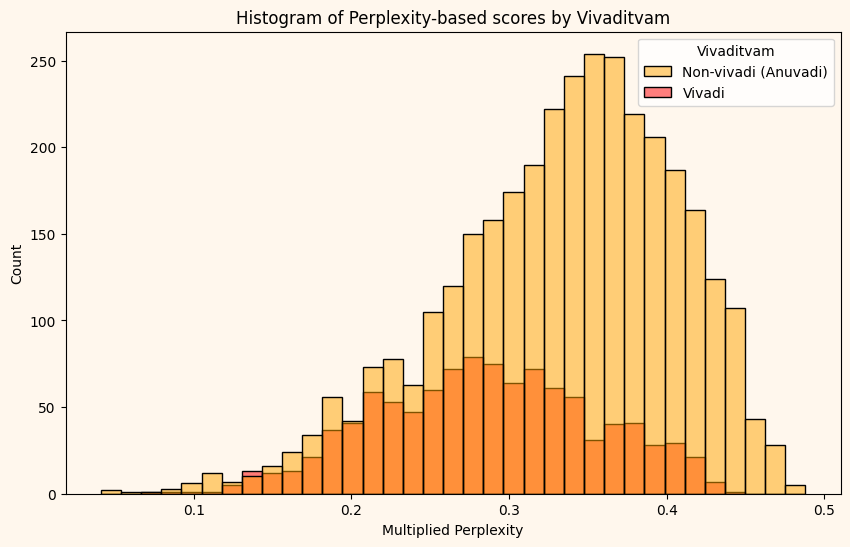
• Ragams that contain the notes G1, R3, N1 or D1 cannot exist without an anchor note i.e. an additional note that supports the given note in the scale. These are called vivadi ragams, explained here nicely. At their modes (peak frequencies), Vivadi ragams are rarer, indicated by their relative closeness to 0 on the y-axis. There is a tussle of score between two competing traits of these ragas. Their scores could be pulled down because there are fewer ragas with these special notes and therefore less likely to be a succeeding note. But its own succeeding note is most likely be its anchor note. It seems, at least near its mode, the former strain won out. Vivadi ragams seem wider spread. It probably means that vivaditvam doesn’t explain a significant part of the scoring.

• The rarest raga with a listed composition is Raga Nadavarangini. The only composition in the raga is krpAlavAla kalAdhara composed by Tyagaraja.

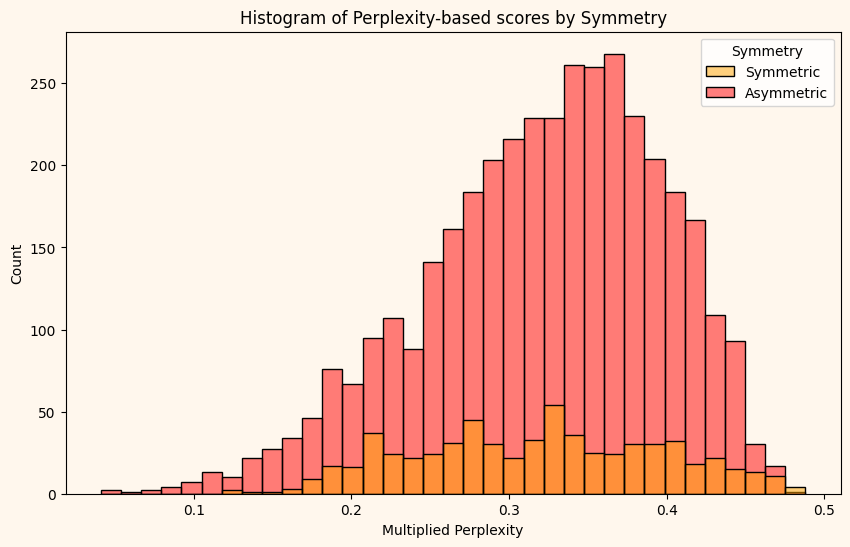
  nAdavarAngiNi:
  - Aarohanam: S P M1 N2 D2 N2 S
  - Avarohanam: S P N2 D2 P M1 G2 R2 G2 S

• As a violinist, I have always felt that symmetric scales felt easier to approach and improvise with. However, that observation is not supported by this whole exercise. Even at the tenth percentile, the scores are not significantly different.

  

  Nevertheless, the rarest raga that is symmetric is Raga Sarvashri, a classic M. Balamuralikrishna three-noted creation:

  sarvashri:
  - Aarohanam: S M1 P S
  - Avarohanam: S P M1 S

• Ironically, Raga Saralam (#1605) is rarer than Raga Gamanaashrama (#76).

Conclusion

Despite a degree of flippancy in my problem statement, these results are genuinely interesting. Yet, I admit that they cannot be correct. There is the issue that different schools learn different scales for the same raga. Even larger is the following: the raga is not its scale. Even if I somehow managed to incorporate other aspects of a raga — jivaprayogas, vadi-samvadis, even something as fundamental as a gamaka — nothing can ever quantify how difficult (or rare) it really must be to explore the ambit of Harikambhoji.

But this approximation does tell us that Harikambhoji and Maalkali have aspects to it that make it special in completely different ways. From at least one point of view, we can appreciate that the melakarta system helps us understand other ragas.

There is a place for mathematics in music. But, in every exclaim, smile, and tear expressed for melody at a concert, you can be assured that none of them were made because of the grammar and science behind the music.

1. Link to my dataset and code: srikanthrajkumar/rareRagas, link to Srihari’s dataset.